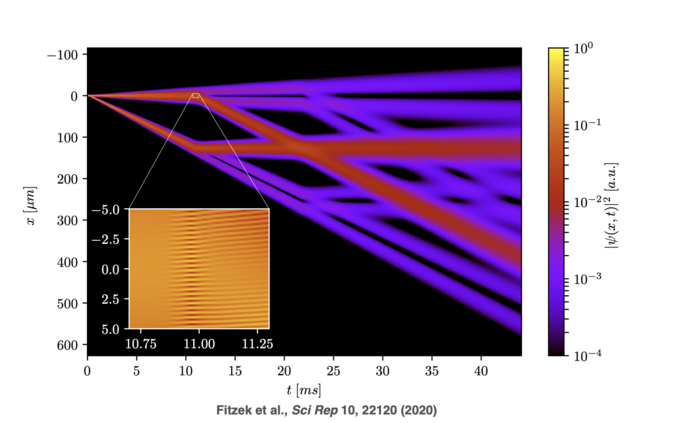
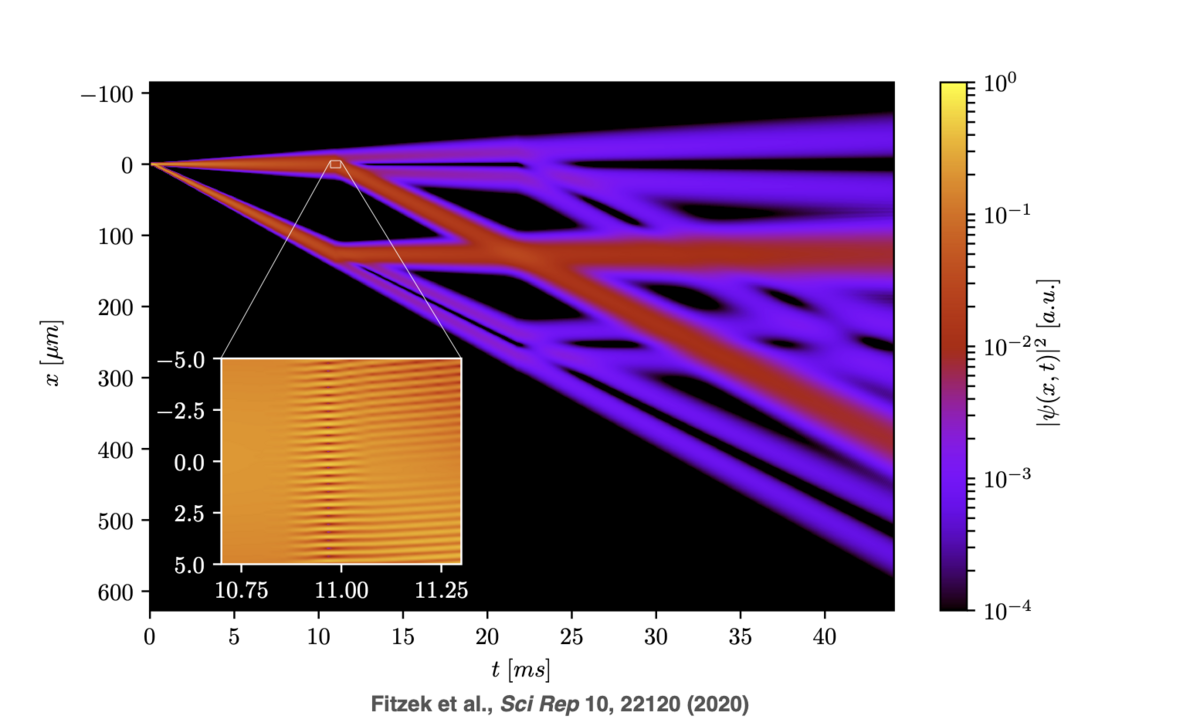
Motivation
Traditional analytic descriptions drastically simplify the dynamics of the atom light interaction. Our position space simulation framework addresses these limitations by discretely sampling the wave function in position space at a high resolution. It then solves the Schrödinger or Gross-Pitaevskii equation for arbitrary potentials in discrete time steps. By relying on much fewer assumptions, it enables us to study a wide range of phenomena that would be difficult or impossible to analyze using traditional methods.
GPU Acceleration
To achieve high simulation speeds, our position space simulation also utilizes graphics processing units (GPUs). This allows us to simulate computationally challenging phenomena, such as Bragg diffraction in trapped 3D geometries, with unprecedented efficiency. A current development version reaches 150ms/step for a 3D wavefunction with 5.3*10^8 grid points in a quadratic potential on an NVIDIA A100 80GiB PCIe.

Realistic simulations of atom interferometers
By providing a baseline truth for various effects, the simulator enables us to validate and refine our analytical descriptions[TODO hyperlink to Theory of Atom Interferometers]. This collaboration between simulation and theory allows us to gain a deeper understanding of complex quantum phenomena. This simulation tool also allows us to model and simulate real-world experiments without having to tailor specific simplifications to enable an analytical treatment. For these see [TODO links to Quantum Gases in microgravitym non-classical states].
The following are examples of the diverse effects that emerge without specific modelling in our position space simulation framework:
- Velocity selectivity: Depending on the pulse characteristics the transfer of atoms between momentum states depends on their velocity.
- Finite momentum widths: Unlike traditional analytic descriptions, our framework can take into account finite momentum widths, providing a more accurate representation of real-world scenarios.
- Multi-port Bragg diffraction: The simulator can model multi-port Bragg diffraction, accurately simulating losses and higher order effects due to that. For a more analytical description that was derived with the support of this framework see [2,3].
- Cross regimes (Raman-Nath to Deep Bragg): Our framework can simulate the whole spectrum between the two pulse parameter regimes Raman-Nath (fast and strong) and Deep Bragg (long and weak) diffraction regimes.
- Bloch oscillations: The simulator can model Bloch oscillations, which are essential for studying the behavior of particles in periodic potentials. This feature was used in [4].
- Mean-field interactions: Our framework takes into account mean-field interactions, allowing us to analyze self interaction in Bose-Einstein condensates and interaction effects between mixtures of different gases. [5]
- Finite pulse time effects: The simulator considers (and even requires) effects that arise from the atom light interactions taking place over a finite duration.
With its ability to capture real-world effects and simulate complex phenomena our position space simulation framework has become an indispensable part of our research arsenal.
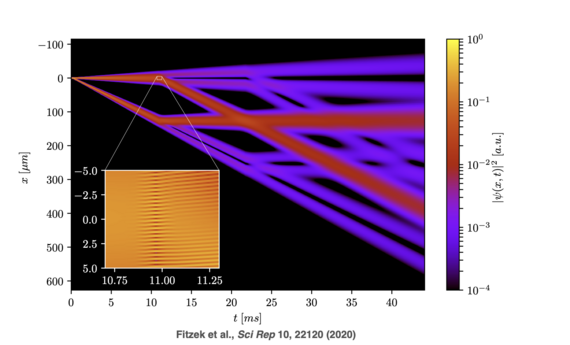
References
[1] Fitzek, Florian, et al. "Universal atom interferometer simulation of elastic scattering processes." Scientific Reports 10.1 (2020): 22120.
[2] Siemß, Jan-Niclas, et al. "Analytic theory for Bragg atom interferometry based on the adiabatic theorem." Physical Review A 102.3 (2020): 033709.
[3] Kirsten-Siemß, J-N., et al. "Large-Momentum-Transfer Atom Interferometers with μ rad-Accuracy Using Bragg Diffraction." Physical Review Letters 131.3 (2023): 033602.
[4] Fitzek, Florian, et al. "Accurate and efficient Bloch-oscillation-enhanced atom interferometry." arXiv preprint arXiv:2306.09399 (2023).
[5] Pichery, Annie, et al. "Efficient numerical description of the dynamics of interacting multispecies quantum gases." arXiv preprint arXiv:2305.13433 (2023).