Introduction
Atom interferometry is a successful tool for precision measurements, inertial sensing and search for physics beyond standard model. Today’s experiments provide the state-of-the-art determination of the fine-structure constant [1,2] and the best quantum test of the universality of free fall [3]. Future matter-wave experiments are anticipated to feature extreme momentum or spatial separations as well as interrogation times on the order of seconds. This will enable them to detect signatures of gravitational waves and aid in the search for dark matter and dark energy [4,5]. Ultimately, however, the performance of any sensor is limited by the accuracy of the theoretical models describing its systematic and the statistical errors. Thus, accurate modelling of these sensors is required to leverage their potential to the fullest.
LMT
Large-momentum-transfer (LMT) beam splitters realize atom interferometers with extreme separations in momentum or space promising unprecedented sensitivities. LMT techniques involve Bragg and Raman scattering that can be combined with Bloch oscillations and cavity-based interferometer schemes. We verify the anticipated metrological gain of these methods by deriving novel theoretical descriptions and developing powerful numerical simulations. This versatile toolbox has enabled us, e.g., to provide accurate theoretical descriptions of the atomic test masses in the case of Bragg diffraction [6,7] and Bloch oscillations [8]. In this context, we also study the effects of Doppler broadening, AC-Stark shift, and polarization errors in retro-reflecting Bragg atom interferometers. These investigations are performed within DFG CRC “DQ-mat” A05 in collaboration with Prof. Klemens Hammerer.
Guided and Trapped
Guiding and trapping of matter waves are paramount for designing extremely sensitive yet compact quantum sensors suitable for real-world applications such as gravimetry [Link to Earth Observation section] and inertial navigation. While continuous trapping allows for multi-axis measurements with long interrogation times in compact dimensions, the interaction with realistic electromagnetic potentials remains a crucial source of decoherence and systematic errors. We develop analytical and numerical models [Ref. to magnetic and optical simulations] to investigate various error sources and design robust guided/trapped configurations ready for real-world applications.
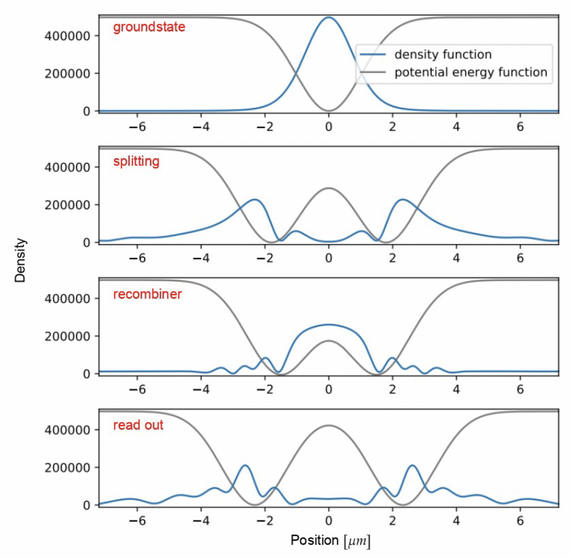
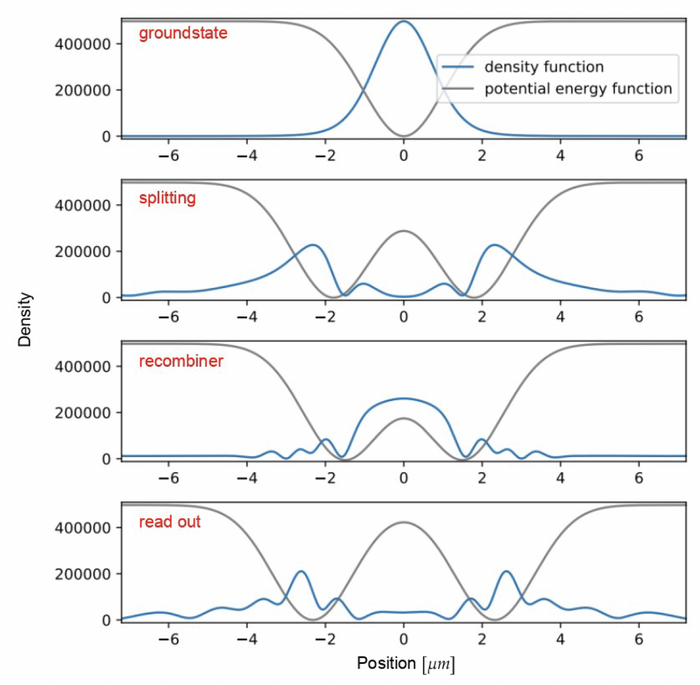
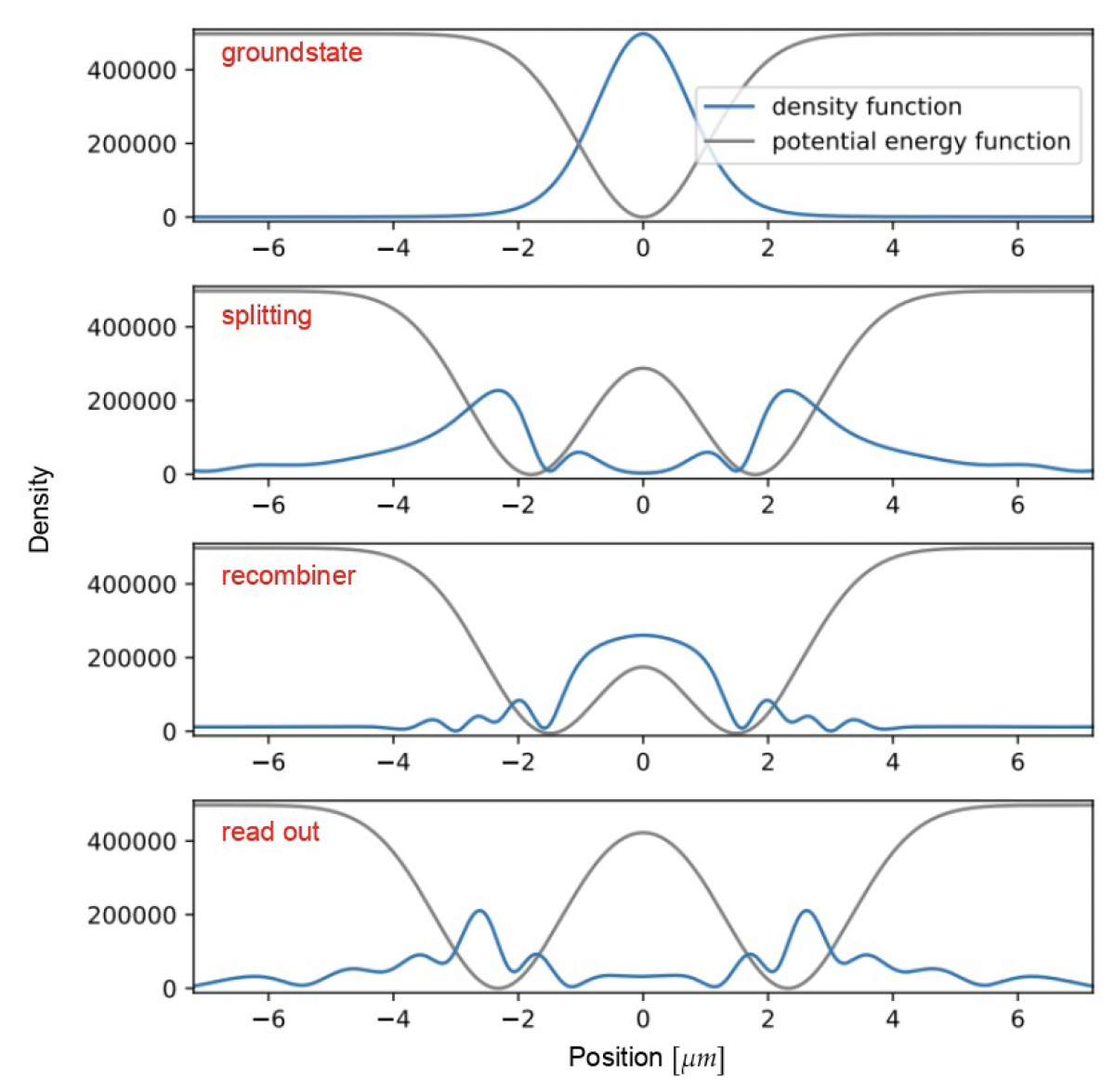
By collaborating together with world’s leading experimental groups in the field, we have established a broad test-ground and a wide applicable area for our theory in various real-life scenarios [9-11].
References
[1] R. H. Parker, C. Yu, W. Zhong, B. Estey, and H. Müller, Measurement of the fine-structure constant as a test of the standard model, Science 360, 191 (2018), URL: https://doi.org/10.1126/science.aap7706
[2] L. Morel, Z. Yao, P. Clad ́ e, and S. Guellati-Kh ́ elifa, Determination of the fine-structure constant with an accuracy of 81 parts per trillion, Nature (London) 588,61 (2020), URL: https://doi.org/10.1038/s41586-020-2964-7
[3] P. Asenbaum, C. Overstreet, M. Kim, J. Curti, and M. A. Kasevich, Atom-Interferometric Test of the Equivalence Principle at the 10−12 Level, Phys. Rev. Lett. 125, 191101 (2020), URL: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.125.191101.
[4] B. Canuel, A. Bertoldi, L. Amand et al., Exploring gravity with the MIGA large scale atom interferometer, Sci. Rep. 8, 14064 (2018). URL: https://doi.org/10.1038/s41598-018-32165-z
[5] L. Badurina et al., AION: An atom interferometer observatory and network, J. Cosmol. Astropart. Phys. 05 (2020) 011, URL: https://dx.doi.org/10.1088/1475-7516/2020/05/011.
[6] J.-N. Siemß, F. Fitzek, S. Abend, E. M. Rasel, N. Gaaloul, and K. Hammerer, Analytic theory for Bragg atom interferometry based on the adiabatic theorem, Phys. Rev. A 102, 033709 (2020), URL: https://journals.aps.org/pra/abstract/10.1103/PhysRevA.102.033709.
[7] J.-N. Kirsten-Siemß, F. Fitzek, C. Schubert, E. M. Rasel, N. Gaaloul, and K. Hammerer, Phys. Rev. Lett. 131, 033602 – Published 19 July 2023, URL: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.033602
[8] F. Fitzek, J.-N. Kirsten-Siemß, E. M. Rasel, N. Gaaloul, and K. Hammerer, arXiv:2306.09399 (15. June 2023), URL: https://arxiv.org/abs/2306.09399
[9] M. Gebbe, et al., Twin-lattice atom interferometry, Nat. Commun. 12, 2544 (2021), URL: https://www.nature.com/articles/s41467-021-22823-8 .
[10] Lachmann, M.D., Ahlers, H., Becker, D. et al., Nat Commun 12, 1317 (2021). URL: https://doi.org/10.1038/s41467-021-21628-z
[11] Ethan R. Elliott, et al., arXiv:2306.15223 (27. June 2023), URL: https://arxiv.org/abs/2306.15223
Funding











